UNIT1-递归下降因为想把作业比较完整地记录下来，而不仅仅是提交一份作业、交差完事，所以会写的相对多一点（可能刚敲完报告的同学 or 已经看了 n 份报告的助教看这篇答辩会觉得很臃肿，但这就不关我事了（？） 博客作业要求部分 包含在 作业完成情况 标题下

作业内容及完成情况

作业要求

指导书总结搬运，回顾用

三次作业任务描述

第一次作业任务：读入一个包含加、减、乘、乘方以及括号（其中括号的深度至多为 1 层）的多变量表达式，输出恒等变形展开所有括号后的表达式。在本次作业中，展开所有括号的定义是：对原输入表达式E做恒等变形，得到新表达式E，且E中不含有字符 ( 和 ) 。
第二次作业任务：读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用的表达式，输出恒等变形展开所有括号后的表达式。本次作业起，不再限制表达式内的括号层数
第三次作业任务：读入一系列自定义函数的定义以及一个包含幂函数、三角函数、自定义函数调用、求导算子的表达式，输出恒等变形展开所有括号后的表达式。

设定的形式化表述

本节按不同作业中课程组的条目标定进行整合；其中，条目前标定**[2]的是第二次作业的新增项目，[3]**同理

表达式 → 空白项 [加减空白项] 项空白项表达式加减空白项项空白项
项 → [加减空白项] 因子项空白项 ‘*‘ 空白项因子
因子 → 变量因子常数因子表达式因子｜[3]求导因子
变量因子 → 幂函数 **[2]**三角函数 [2]自定义函数调用
常数因子 → 带符号的整数
表达式因子 → ‘(‘ 表达式 ‘)’ [空白项指数]
幂函数 → 自变量 [空白项指数]
自变量 → ‘x’ ‘y’ ‘z’
**[2]**三角函数 → ‘sin’ 空白项 ‘(‘ 空白项因子空白项 ‘)’ [空白项指数] ‘cos’ 空白项 ‘(‘ 空白项因子空白项 ‘)’ [空白项指数]
- 请注意输出三角函数时需要满足的形式化表述：内部元素为因子
指数 → ‘**‘ 空白项 [‘+’] 允许前导零的整数
- 指数一定不是负数，且输入的指数不得超过8
带符号的整数 → [加减] 允许前导零的整数
允许前导零的整数 → (‘0’’1’’2’…’9’){‘0’’1’’2’…’9’}
空白项 → {空白字符}
空白字符 → （空格） \t
加减 → ‘+’ ‘-‘
[2]自定义函数定义 →→ 自定义函数名空白项 ‘(‘ 空白项自变量空白项 [‘,’ 空白项自变量空白项 [‘,’ 空白项自变量空白项]] ‘)’ 空白项 ‘=’ 空白项函数表达式
- 规定自定义函数在表达式输入前进行输入，需要预先输入自定义函数数量，且0\le num\le3
[2]自定义函数调用 →→ 自定义函数名空白项 ‘(‘ 空白项因子空白项 [‘,’ 空白项因子空白项 [‘,’ 空白项因子空白项]] ‘)’
**[2]**自定义函数名 →→ ‘f’ ‘g’ ‘h’
**[2]**函数表达式 →→ 表达式
- 第三次作业函数表达式中可以调用其他自定义函数，但保证不会出现递归调用的情况；同时调用自变量为常数的自身也不被允许)
**[3]**求导因子 →→ 求导算子空白项 ‘(‘ 空白项表达式空白项 ‘)’
**[3]**求导算子 →→ ‘dx’ ｜’dy’ ｜’dz’

作业完成情况

虽然笨人很喜欢写东西，但耐不住笨人就是菜，三次作业全有bug（寄）

第一次作业

架构设计

简单分析过题面之后，可以分析出一个初步的构造顺序：表达式项因子表达式\to项\to因子再进行进一步分析后，可以发现题目中最基础的单元就是一个形如a*x^b*y^c*z^d形式的单项式，而无论是题干中出现的任何一种构成成分，都由一个或多个这样的单项式构成：

常数因子\to带符号整数：b=c=d=0
变量因子\to幂函数：a\ne0\ \&\&\ bcd中仅存在一个值\ne0
表达式：若干单项式相加
因子：若干单项式相加
项：若干单项式相加前三个条目的安排相对直观，那为什么因子也需要用若干单项式相加来表示呢？原因在于这里没有写下的一条构成路线：

因子表达式因子表达式

也就是说，表达式的组成也可以成为因子的一种，也容易理解： (2x+y+1)按照形式化表述显然属于因子，然而很明显其无法用一个单项式表示而对于项，则由组合规则同理可知，不再赘述于是第一次设计采用了：

数据结构：统一的HashSet<Values> values字段存储对应条目的值，每一个Values都表达一个单项式；
- 使用HashSet这种不能便利取值的容器是第二次的罪魁祸首
计算方法：HashSet.add()方法表示相加，创建一个两重遍历容器的方法表示相乘
类与方法：

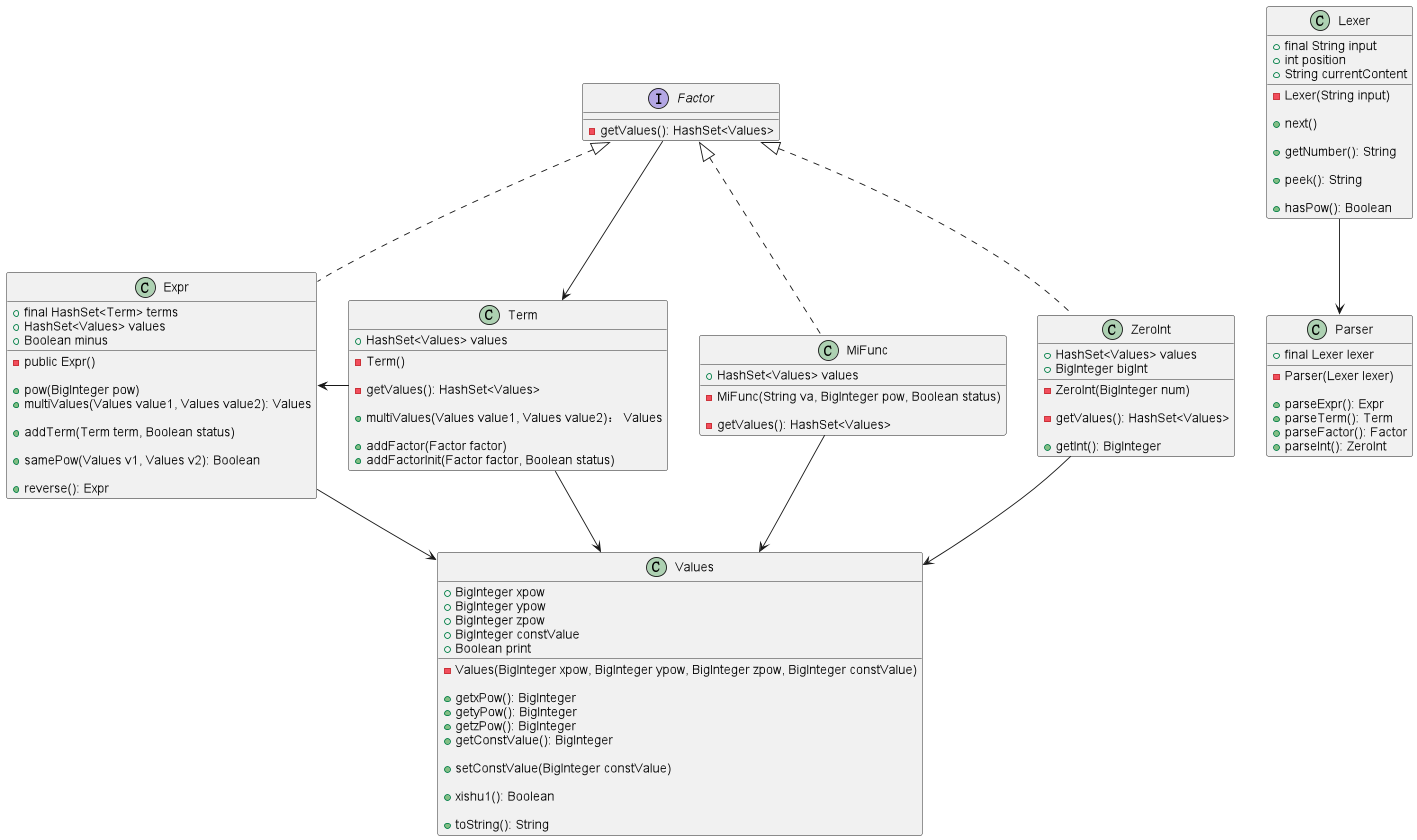
实现过程/难点

词法分析器Lexer：构建思路来自单元训练栏目，根据当前字符判断元素种类，再决定Paser的解析逻辑，考虑各种可能出现的字符才能避免解析时出现Runtime Error（换句话说，一般RE的话就是解析错了，或者是爆递归栈、爆堆等，结构不是很怪的话比较少见）
符号与减法：直到很靠后的时候才想出去解析可能出现负号位置（共三个）的解决方案：先查询一下是不是负号，然后给一个标记位，控制到最后返回的表达式/项/因子的系数正负
乘法实现：开始直接把两项add到一个容器了，后来才意识到需要按照分配律一项一项的加指数再add
指数与 **0：n次方就把前面的元素乘个n次
- 特判0**0=1（三角函数特判，易锅）
化简-合并同类项：每次add时，遍历所有容器内已有元素，如指数完全一致则进行系数运算并放弃add操作；否则直接add
输出：为Values类配置了ttoString()方法，不重写原有的toString方法（出过锅），输出最终表达式中所有Values的ttoString()字符串
复杂度图：

debug与测试

强测得分/互测失分/互测得分：100/1(1bug)/0.75(1bug)
互测锅是后导空白字符，会一直解析直到OutofIndex报RE，挑战最短hack数据之：x<space>
- 解决方案是预处理所有空白字符，忍痛在递归下降里用字符串处理，写了replaceAll
互测刀到的是如果有形如factor*a，且a.length\ge2时，会只乘以贴近乘号的值
性能方面：x*x要比x**2短一个字符，x-1要比-1+x短一个字符，处理好这个优化点就能强测100了（确信
- 不要随便对输出用正则：
- 消去1*x的无用系数，导致21*x\to 2x
- 替换长的x**2为等价描述，导致x**21\to x*x1

第二次作业

架构设计

TLE，遂重构。 很遗憾，对于上一次的遍历查询值的操作来说，2s的CPU时间很明显不够祸祸的，所以只能换成Map类型便于查询 Map类型就要考虑采用什么作为key/value进行匹配，我采用了<String, Values>的键值对进行适配，为每一个项创建一个独特的字符串，且能够合并的项需要保证字符串相同（合并同类项时使用）于是增添了一个新的hashString()方法，为每个Values创建字符串（生成key），这样其中的键值对都是<Values.hashString(), Values>形式的了；具体而言需要输出除了系数外的所有信息（xyz指数，三角函数的种类、指数、内部表达式、数量）。这也是这次重构中我遇到的的主要难点 其次是三角函数引入对Values类造成的改变，为了保证项中仅含单个三角函数时也能进行合并，故也采用类似Values的结构构建，键值对类型相同，此处的String则指三角内expr的hashStringInValues()（必须保证系数也一并输出，否则sin(x)和sin(2*x)将能合并）最终结构为

实现过程/难点

hashString()方法：由于采用字符串比较，所以需要严格保证能够合并的项需要保证字符串相同这一要求，否则无法合并。那么就需要避免出现2*cos(x-1)和-3*cos(-1+x)不能合并的惨案。最简单有效的办法就是保证expr有序，这也是为什么最后架构采用了TreeMap<String, Values>（其实这里同时做了诱导公式，保证三角内expr第一项恒为正，避免了上述无法合并的情况）
三角函数化简 - 特殊值：对于特殊值，也就是cos(0)=1、sin(0)=0；务必注意(sin(0))**0=1，不过我是在创建三角函数时就进行了其中expr特判，如果expr.values = 0就会返回0/1，而不是sincos，转化计算的优先度要高于乘方
三角函数化简 - 诱导公式：已在hashString()方法中进行了解释
三角函数化简 - 二倍角：对于二倍角优化比较复杂，简化下只处理了指数为1的sin二倍角和指数为2的cos二倍角/平方和
自定义函数与调用：创建类ArtiFunc用于存储函数相关数据，在自定义函数调用时解析对应函数名、因子，同时使用字符串替换原公式形参后直接进行完整公式的解析，并返回TreeMap <String, Values>
- 在调用时才进行解析的做法可以有效避免被根本不调用的超高cost自定义函数刀掉
复杂度图：

debug与测试

bug点：
- 自定义函数实参因子替换后，需要给因子加一层括号，否则可能会出现sin(f(x))\to sin(x*y)这样不符合形式表达的bug
- 三角函数优化太容易出锅了，尤其是引入了新的机制hashString()，即使二倍角优化更改的是三角函数中某一个expr的值，但最后需要把整个Values的hashString()再存一遍（更新），经常在运算忘记更新导致合并出锅，反向优化甚至错误输出
- 在优化过程中需要不断把合并掉的三角函数从容器中取出、运算、装入，这个过程需对元素进行深克隆，出锅后细化了Calculator类，支持了各种元素的深克隆方法（尽可能同名以减轻记忆压力）
- 输出时，三角函数套括号的层数判断出了问题，具体为编写的hasOneFactor()判断不严谨，没有考虑到a*sin(a^{‘})的情况，仍然会输出一层括号，导致格式不合法
强测得分/互测失分/互测得分：88.7/1(1bug)/4.75(4bug)
强测（20测试点）2×0分，4×性能非满分
互测则全是优化的问题，bug修复就注释了四行优化函数摆了烂，下来还是好好修了修；
刀到的是自己写了随机数据的测评姬，同时SymPy房里所有人的输出，谁不一样就拎出来批（×），bug还算比较多的
小提示：别卷优化

《你在强测中得到了 88.7702 分。》 架构设计 第三次作业的实现在上一次作业的合理基础上反而更加简单，只需要实现求导功能和自定义函数相互调用两点即可求导方法函数增添在原有的计算类Caluculator中，接受TreeMap<String, Values>，对每个单项的Values求导后返回一个盛放导数的新容器自定义函数由于支持了声明时嵌套，所以为了使用简洁，改成了在声明时预解析的方式处理，但这样虽然方便处理函数，但没法解决第二次作业提到的高cost互测数据，有TLE/MLE风险类与方法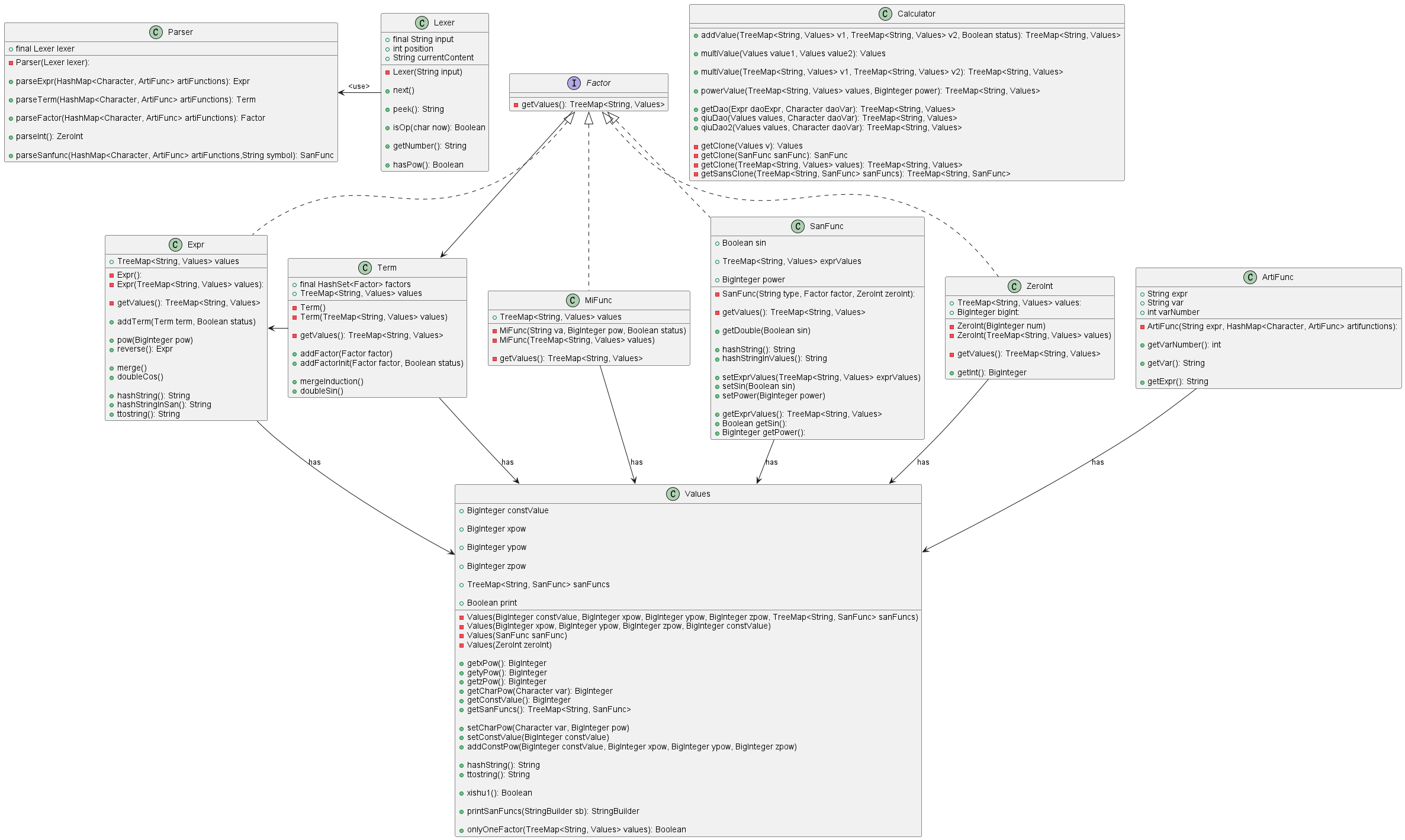： name 实现过程/难点

求导功能：修改Lexer支持解析求导文法，并在Calculator类中创建求导方法，返回输入TreeMap<String, Values>的导数；
- 为便于实现，我将求导功能分类，分别实现基础项a、a*x^b、sincos(expr)和可递归项的求导(sincos(expr))**e、sincos(expr1)*sincos(expr2)、x^b*sincos(expr1)[*sincos(expr)]?
自定义函数：只需提前解析自定义函数内容即可，注意替换调用时的因子对应
复杂度图：

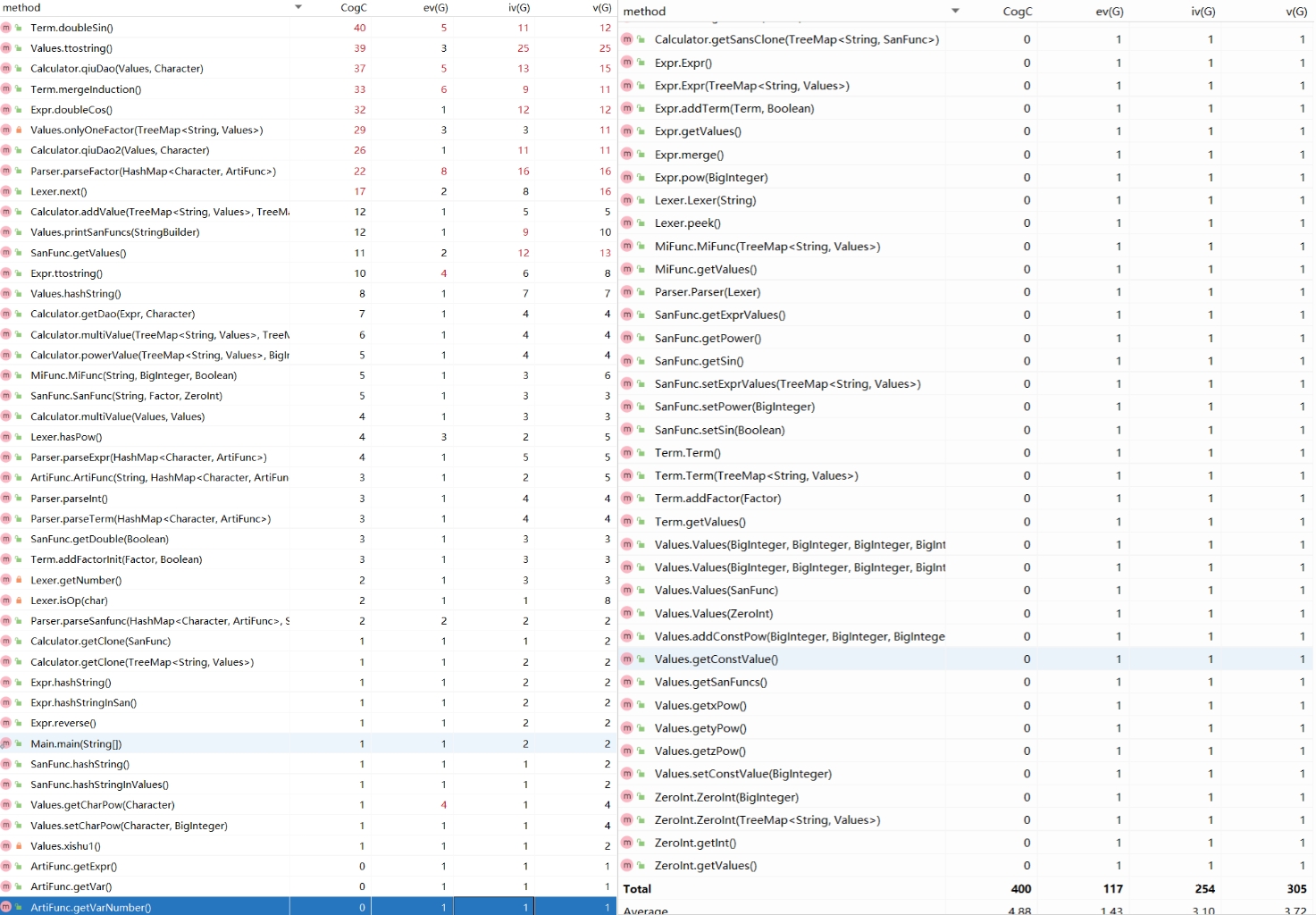
debug与测试

bug点：
- 递归部分的求导函数，复杂的判断条件以及繁琐的操作（取出、运算、更新、放回等）使得方法复杂度远超其他方法，回想起来，编写的时候实际上也很头疼，出错其实也不出意外
- 三角函数因子内含有自定义函数调用，这种组合可能会出现仅用一层括号就包住一个表达式的情况，然后在解析过程中就会因为文法问题出锅；解决方案是在输出自定义函数调用结果时也用一层括号包起来，表达式\to表达式因子，使其符合三角函数形式化表述
强测得分/互测失分/互测得分：85.7/3(2bug)/1(1bug)
强测（15测试点）2×0分，1×性能非满分
小提示：别卷优化

《你在强测中得到了 85.72 分。》

作业总结

首先要感谢上学期的先导课，有先导课做Java语言的基础极大地便利了我对基础语法的理解与运用，尤其是在第一次作业上，没有犹豫太多就选择了相对能够满足当前要求的架构（虽然后续需要重构，但完成了当时任务的要求）。其次，本单元作业通过构造一系列类间关系进行表达式的解析，使用了部分接口、继承、重写等Java语言特性。再其次，这次作业为递归下降的原理做了引入和解释，对之后的编译原理也许有一定助力作用

设计模式思考

在第一次作业中因为实现的功能比较简单，就没有涉及到深/浅克隆的处理；但是随着计算功能复杂化、容器深度变深（Values内又存放了Map类），深克隆逐渐重要了起来。虽然应该写序列化深克隆方法，但是当时完全忘记了clone方法能重写（），然后又造了轮子功能类（计算类）与数据类（表达式组件类）要进行明确划分，避免一个类同时运行多种复杂函数。从第二次作业重构起，创建了一个单独的运算类Calculator，用于执行乘法、乘方功能，并在第三次作业中把求导功能也一并集成，反思这个设定应该为每一种运算创建一个类，避免Calculator类过于复杂。同时写的东西实际上没有写成静态方法（知识储备不足），导致每次计算都要new一个对象，虽然没有字段但也对运行时间、空间有一定的影响。

代码复杂度分析

肉眼可见的，复杂度飘红的方法都是功能复杂的方法，如[1]中的toString、pow方法；[2]中的doubleSin、mergeInduction方法、[3]中的qiuDao方法。同时，出锅的实际上也正是这几个方法，几乎无一幸免。所以在编写代码的过程中要尤其注意行数多、判断循环条件复杂、功能复杂的方法，尽量将其功能分散、模块化，或者说可以方法多，别让方法难，否则单个复杂方法debug过于折磨，而多设方法、接口处还能进行调试检测，方便缩小错误范围。

互测总结

各次作业中强测出现的bug已在各自的debug与测试栏目中进行分析。对于互测部分，hack他人代码主要依靠自己随机递归思路生成数据+借助SymPy库实现的校对测评姬。

纯多项式使用expand进行比对、含三角函数则输出式相减与0比较，如遇合并项则选择人工核对（这里其实可以代入变量值进行比对，不过没写.jpg）只能说自己写的逻辑确实不容易hack到自己，第一次作业的测评姬甚至不支持生成末尾空格，所以根本测不出来自己的bug；

前期的数据空有一番大体量，但是覆盖度并不好，总有组合测试不到；后面改良版本则更多侧重0、±1等边界小数据是否会出现错误。对于三角函数合并、求导，以及求导后再进行的合并化简，我设计了一个占比不同的导数内表达式生成机制，能够较充分地覆盖各类情况进行测试（能出现含0层三角函数的项，同时也按照等比的概率考虑到了多重三角函数嵌套的可能性和概率的合理性）对于导数，应该生成：