第 01 讲 渐进记号

表示时间、空间复杂度时会采用一系列符号来表示其对应的数量级

  • $O$：渐进上界，表示算法复杂度的上限，算法执行时复杂度不会超过这个值（实际上也是估算，常数级不予考虑）
  • $\Omega$：渐进下界，表示算法复杂度的下限，通常表示最优情况下的复杂度
  • $\Theta$：渐进紧确界，当 $O$ 和 $\Omega$ 相等时，对应的值就被记为 $\Theta$，表示算法的性能浮动
img

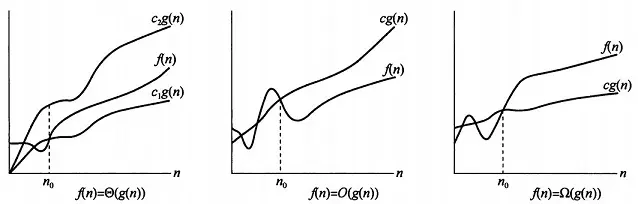
这张图中 $f(n)$ 代表算法的实际运算，可以看到当自变量 $n$ 足够大时，$O>f>\Omega$ 的关系相对明确，也间接说明了渐进上下界的概念


第 02 讲 复杂度分析

分析递归的时间复杂度可以使用三种方式：递归树法、代入法、主定理法

递归树法

递归树法主要计算的是树的深度，最终的时间复杂度是深度乘以每层的复杂度得到的积。

image-20230916152237825

如上图中每层的复杂度都是 $O(n)$，同时每一个分支进入每一层都要变为一半，选取随意一支，计算 $1 = n*(\frac 1 2)^{k}$，得到 $k=log_2n$，最终换底提出系数，算出深度为 $log\ n$ 层。当各个分支分得的复杂度不同时，要选取下降最慢（复杂度最高）的一条分支进行计算，保证覆盖度。

代入法

代入法从数学方向证明复杂度，过程中先进行猜测，再找出对应复杂度的系数，利用数学归纳法证明复杂度的猜测成立。但当猜测解不容易得到时比较困难

image-20230916202852221

主定理法

主定理法能够将常用的公式对应的递归式分析得出通解，形式简洁，但其使用范围有限，需要递归式满足特定情况才可以使用。
$$
T(n)=aT(\frac n b)+f(n)\
T(n)=\begin{cases}
\Theta(f(n)) & if\ f(n)=\Omega(n^{log_ba+\epsilon})\
\Theta(n^{log_ba·logn}) & if\ f(n)=\Theta(n^{log_ba})\
\Theta(n^{lob_ba}) & if\ f(n)=O(n^{log_ba-\epsilon})
\end{cases}
$$
简单来说，如果 $f(n)$ 的数量级要比 $n^{log_ba}$ 大，那么时间复杂度就取决于更大的 $f(n)$；若同数量级则是乘以 $log\ n$；若 $f(n)$ 更小，则体现为 $n^{log_ba}$ 的数量级。当 $f(n)=n^k$ 时，可以进一步简化：
$$
T(n)=\begin{cases}
\Theta(n^k) & if\ k > log_ba\
\Theta(n^·klogn) & if\ k = log_ba\
\Theta(n^{lob_ba}) & if\ k < log_ba
\end{cases}
$$
当主定理中 $f(n)$ 的部分处于 $[n^{log_ba-\epsilon},n^{log_ba+\epsilon}]$ 之间，同时不等于 $n^{log_ba}$ 时（也就是比 $n^{log_ba}$ 大，但是又不大出一个 $n$ 的数量级，比如 $nlogn$），不能应用主定理的任意一项，这时需要使用拓展形式：
$$
T(n)=\Theta(n^{log_ba·log^{k+1}n})\
if\ f(n)-\Theta(n^{log_ba·log^kn})
$$


第 03 讲 分治思想

分治（Divide-and-Conquer）

分治思想（D&C）是计算机中一种重要的处理问题的思想，它首先将给定的问题进行分割，划分出多个子问题（通常是近似规模的），再对各个问题逐个解答（考虑递归处理），最终把子问题的解整合为所给问题的解

归并排序（Merge Sort）

  • 合并策略：当输入为多组有序数组时，对其进行两两合并，并在过程中保持其有序性，最终合并得到所有元素的有序序列，完成排序流程；
    • 当输入完全无序时，将数组的长度降低为 $1$，此时每个数组（单个元素）都必定有序，由此开始进行合并的排序方式，这就是归并排序
  • 归并排序将整个无序数组进行拆分，划分为局部有序的数组（单一元素），再进行数组间两两的排序，最终实现对整体元素的排序；划分这一过程是分治思想的重要体现

归并排序流程

  • 将数组 $A[1, n]$ 排序的问题分解为数组 $$A[1, |\frac n 2|]$$ 和 $A[|\frac n 2|, n]$ 的排序问题
  • 递归解决分解后的子数组排序问题，并得到有序的子数组
    • 递归边界为数组长度为 $1$ ，此时单元素数组天然有序
  • 最终将子数组反向合并为有序数组
  • 伪代码实现：
// 主函数调用：MergeSort(A, left, right)
// 终止递归的边界条件
if (left >= right) {
    return A[left, right]
}
mid = (left + right) / 2
// 排序左侧数组
MergeSort(A, left, mid)
// 排序右侧数组
MergeSort(A, mid + 1, right)
// 将两数组排为一个有序数组
Merge(A, left, mid, right)
return A[left, right]
// 具体排序函数：Merge(A, left, mid, right)
// Input: A[1, n]
// Output: A[left, right] ( sorted array )
B[left, right] <- A[left, right]
    
// 初始化指针
i = left, j = mid, k = 0
    
// 数组 1：0~mid，数组 2：mid+1~right （均分别有序）
while (i <= mid && j <= right) {
    // 比较 i & j，谁小就在 A 的后面放下
    if (B[i] <= B[j]) {
        A[left + k] = B[i]
        i++, k++
    } else {
        A[left + k] = B[j]
        j++, k++
    }
}

// 其中一个数组输入完了，把剩下的大数全插入
if (i <= mid) {
    // i 没完，j 完了，把数组 1 剩余的元素插在后面
    A[left+k, right] = B[i, mid]
} else {
    // j 没完，i 完了，把数组 2 剩余的元素插在后面
    A[left+k, right] = B[j, right]
}

// 排序完毕，返回结果
return A[left, right]
  • 子过程由于相当于只遍历了一遍 $A$ 数组，故单轮排序的时间复杂度为 $O(n)$

复杂度分析

设 $n$ 个元素的 MergeSort 函数的运行句数为 $T(n)$，则有
$$
T(n)=\begin{cases}
2*T(n/2) + O(n)\
O(1)
\end{cases}
$$
对整个过程画出递归树，分别计算每个节点的时间复杂度：

image-20230916152237825

观察可以得到，每一层的复杂度都为 $O(n)$，同时纵向共有 $log\ n + 1$ 层（计算深度为 $log\ n$），相乘则可得到总时间复杂度：
$$
T(n)=O(nlog\ n)
$$

最大子数组（Maxinum Contiguous Subarray）

  • 最大子数组问题给定一个实数数组 $A[n]$，其中任意元素不限制其正负，我们需要寻找保持连续的子数组 $A[i, j]$，要求其元素和在所有的子数组中最大

暴力（Brute Force）流程

  • 求出每个合法的 $i$ 和 $j$ 的组合，并更新维护子数组和的最大值
  • 遍历 $i$、$j$ 和子数列的每一项，易知其为 $O(n^3)$ 的算法

数据重用（Data Reuse）流程

  • 发现每次计算子数组和时并不需要每次都从第一个元素开始加起，因为有：

$$
A[i, j]=A[i,j-1]+A[j]
$$

  • 也就是说保存每次计算的 $A[i,j-1]$ 再加上一个新元素就能够实现子数组和的计算，易知其为 $O(n^2)$ 的算法

归并算法

在数组中部划线将其分割为两部分，则最大子数组必定从以下三部分之中取得：线左侧的数组、线右侧的数组、跨越线的数组

  • 跨线的数组由于必定包括线左右的元素，可以以此分别向两侧遍历，获得最大的跨线数组
  • 左右单侧的数组可以通过递归主过程来寻找，直至数组变为单个元素返回结果
  • 算法复杂度为 $O(n·logn)$

堆排序

堆的性质

  • 根节点命名为 1
  • 对于任意节点 $i$
    • 左儿子为 $2i$
    • 右儿子为 $2i + 1$
    • 父节点为 $[\frac i 2]$
  • 堆中的每个三角形都要满足父节点小于儿子节点

插入操作：

  • 在堆的末尾插入一个元素
  • 与父节点做比较，如果自身更小，则与父节点交换位置
  • 循环第二步直至成为树根节点，或自身比当前的父节点大

取出操作：

  • 取出树根节点，将堆中的最后一个元素放置在根节点位置
  • 与儿子节点比较，如果自身大于一个儿子则进行交换
  • 循环第二步，直至成为叶子节点，或自身比两个儿子节点都小

堆排序

  • 以堆为数据结构进行的排序方式，堆的插入元素、取出最小元的时间均为 $O(log\ n)$，建堆的时间是 $O(n·log\ n)$
  • 建堆可以优化为 $O(n)$ 的复杂度：先任意建立树形，再对每个非叶子节点进行大小比较的向下调整，调整过程中，深度越大的节点调整的次数越少（节点数也更多），越往上调整的次数越多

伪代码

  • 非正式语言，表达算法的本质，但不拘泥细节；反映算法的流程，但不过于繁琐

书写约定：

  • 定义算法的输入和输出
  • 循环、条件等语句块需要缩进
  • 赋值语句统一形式（等号、箭头）
  • 注释使用 //